2 Affine Stereo
2.1 Perspective and projective camera models
The full perspective transformation between world and image
coordinates is conventionally analysed using the pinhole camera model,
in which image-plane coordinates (u, v)
are ratios of world coordinates
(xc,
yc,
zc)
in a camera-centred frame, thus:
u = fxc/zc,
v = fyc/zc.
The relation between the camera-centred and some other world coordinate frame
consists of rotation (R) and translation (t)
components representing the camera's orientation and position.
Using homogeneous coordinates (with scale factor s for convenience),
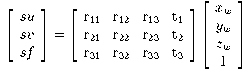 (1)
(1)
The relation between image plane coordinates (u, v) and
pixel addresses (X, Y) can be modelled by an affine
transformation
(to represent offsets, scaling and shearing).
Combining this with (1) yields a general 3D
to 2D projection, with 11 degrees of freedom:
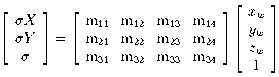 (2)
(2)
This is the usual camera model for many stereo vision systems.
Although it neglects effects such as lens distortion which are
significant in some high-accuracy applications
[15],
it correctly predicts image distortion due to
perspective effects e.g. parallel 3D lines projecting to
intersect a vanishing point and the cross ratio (not ratio) of
lengths is invariant to this transformation.
2.2 Weak perspective and affine camera models
Consider a camera viewing a compact scene of interest from distance h.
For convenience, we can translate the world coordinate
system so that the scene
lies close to the world origin. The component of t
along the optical axis, t3,
will then equal h. As distance
increases relative to the extent of the scene, sf / h
will tend to
unity for all points, and equation (2) becomes:
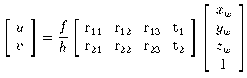 (3)
(3)
This formulation assumes that images are not distorted by variations
in depth, and is known as weak perspective
[13]. It
is equivalent to
orthographic projection scaled by a factor inversely proportional to
the average depth, h.
It can be shown that this assumption results in an error which is, at worst,
Delta(h)/h times the scene's image size.
The entire projection, again incorporating scaling and
shearing of pixel coordinates, may now be written very simply as a
linear mapping:
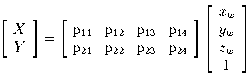 (4)
(4)
The eight coefficients
pij
efficiently represent
all intrinsic and extrinsic camera parameters
[15].
This simple approximation to the projection transformation
- the affine camera [11] - will
be used as the camera model throughout the paper. Its advantages
will become clear later when it leads to efficient calibration
and reduced sensitivity to image measurement error.
Note that parallel lines project to parallel lines in the image
and ratios of lengths and areas are invariant to the transformation.
2.3 Motion of planar objects under weak perspective
There are many situations in computer vision where an object must be
tracked as it moves across a view. Here we consider the simple,
but not uncommon, case where the object is small and has planar
faces.
We can define a coordinate system centred about the object face
itself so that it
lies within the xy plane. If the object is small compared to the
camera distance, we again have weak perspective, and a special case
of (4):
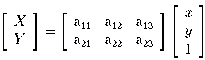 (5)
(5)
We see that the transformation from a plane in the world to the image plane
is a 2D affine translation.
As the camera moves relative to the object, parameters
aij
will
change and the image will undergo translation, rotation, change in
scale (divergence) and
deformation, but remain affine-invariant
[8,
2]
(figure 1).
This is a powerful constraint that can be exploited when tracking a
planar object. It tells us that the shape of the image will deform
only affinely as the object moves, and that there will exist an affine
transformation between any two views of the same plane.

Figure 1: The gripper being tracked as it translates and
rotates under weak perspective.
The origin and sampling points of the tracker are shown in
white.
The front of the gripper is approximately planar, and its
image shape distorts affinely as it moves under weak perspective.
2.4 The affine stereo formulation
In stereo vision two calibrated views of a scene from known
viewpoints allow the Euclidean reconstruction of the scene.
In the following two uncalibrated views
under weak perspective projection are used to recover
relative 3D positions and surface orientations.
Recovery of relative position from image disparity
We assume that the cameras do not move relative to the scene during
each period of use.
Combining information from a pair images, we have four image
coordinates
(X, Y, X', Y')
for each point, all linear functions of
the three world coordinates
(xw,
yw,
zw):
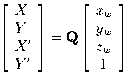 (6)
(6)
where
Q is a 4*4 matrix formed
from the
pij
coefficients of equation (4)
for the two cameras.
To calibrate the system it is necessary to observe a minimum of
four non-coplanar reference points, yielding sixteen
simultaneous linear equations from which Q may be found.
With noisy image data, greater accuracy may be obtained by
observing more than four points.
Once the coefficients are known, world coordinates can be
obtained by inverting (6), using a least-squares method to
resolve the redundant information. Errors in calibration will manifest
themselves as a linear distortion of the perceived coordinate
frame.
Note:
It is not essential to calibrate a stereo vision system to obtain useful
3-D information about the world. Instead, four of the points observed
may be given arbitrary world coordinates (such as (0, 0, 0), (0, 0, 1),
(0, 1, 0) and (1, 0, 0)). The appropriate solution for
Q will define a coordinate frame which
is an arbitrary 3-D affine transformation of the `true' Cartesian frame,
preserving affine shape properties such as ratios of lengths and
areas, collinearity and
coplanarity. This is in accordance with Koenderink and van Doorn's
Affine Structure-from-Motion Theorem
[9].
In hand-eye applications, it might instead be convenient to calibrate
the vision
system in the coordinate space in which the manipulator is controlled
(assuming this maps approximately linearly to Cartesian coordinates).
This can be done by getting the robot manipulator to move to
four points in its workspace.
The integration of information from more than
two cameras to help avoid problems due to occlusion
is easily accommodated in this framework. Each view
generates two additional linear equations in (6)
which can be optimally combined.
Recovery of surface orientation from disparity gradients
Under weak perspective any two views of the same planar surface will
be related by an affine transformation
that maps one image to the other. This consists of a
pure 2D translation encoding the displacement of the centroid
and a 2D tensor - the disparity gradient tensor
- which represents the distortion in image shape.
This transformation can be used to
recover surface orientation [2].
Surface orientation in space is most conveniently represented by a
surface normal vector n. We can obtain it by the vector
product of two non-collinear vectors in the plane which can
of course be obtained from three pairs of image points.
There is, however, no redundancy in the data and this method
would be sensitive to image measurement error. A better
approach is to exploit all the information in available in the
affine transform (disparity field).
Consider the standard unit vectors X and Y
in one image
and suppose they were the projections of some vectors on the object surface.
If the linear mapping between images is represented by a 2*3
matrix A, then the first two columns of A itself will
be the corresponding vectors in the other image.
As the centroid of the plane will map to both image centroids, we can
easily use it and the above pairs of vectors to find three points in
space on the plane (by inverting (6))
and hence the surface
orientation.
Next
Appendix
Contents
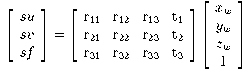 (1)
(1)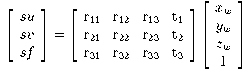 (1)
(1)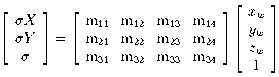 (2)
(2)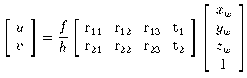 (3)
(3)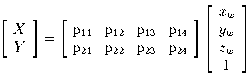 (4)
(4)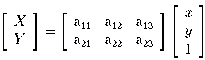 (5)
(5)
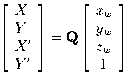 (6)
(6)