3 Tracking using affine active contours
An active contour (or `snake') [7]
is a curve defined in the image plane that moves and deforms according
to various `forces'. These include external forces, which
depend on local image properties and are used to
guide the active contour towards the image features,
and internal forces which depend on the contour shape
and are used to enforce smoothness.
Typically, a snake will be attracted to maxima of image intensity
gradient, and used to track the edges of a moving object.
3.1 Anatomy
Our model-based trackers are a novel form of active contour.
They resemble B-spline snakes [3] but consist of (in the order
of 100) discrete sampling points, rather than a smooth curve
[6].
We use them to track planar surfaces bounded by
contours, on the robot gripper and the object to be grasped.
Pairs of trackers operate independently in the two stereo views.
The trackers can deform only affinely, to track planes viewed under weak
perspective [1].
This constraint leads to a more efficient
and reliable tracker than a B-spline snake, that is less easily
confused by background contours or partial occlusion.
Each tracker is a 2D model of the image shape it is tracking, with
sampling points at regular intervals around the edge. At each sampling point
there is a local edge-finder which measures the offset between
modelled and actual edge positions in the image, by searching for the
maximum of gradient along a short line segment [5].
Due to the so-called aperture problem
[18], only the normal
component of this offset can be recovered at any point
(figure 2).
The positions of the sampling points are expressed in affine
coordinates, and their image positions depend upon the tracker's
local origin and two basis vectors. These are described by six
parameters, which change over time as the object is tracked.
The contour tangent directions
at each point are also described in
terms of the basis vectors.
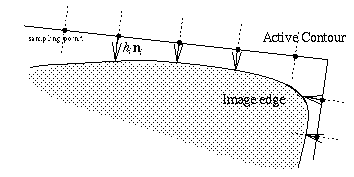
Figure 2:
An active contour.
The image is sampled in segments normal
to the predicted contour (dotted lines) to search for the maximal
gradient. The offsets between predicted and actual edges (arrows)
are combined globally to guide the active contour towards the
image edge.
3.2 Dynamics
At each time-step the tracker moves and deforms to minimise the
sum of squares of offsets between model and image edges
hi. In our
implementation this is done in two stages. First the optimal
translation is found, then the deformation, rotation, scale (divergence)
components are calculated. Splitting the task into these two stages
was found to increase stability, as fewer parameters were being
estimated at once.
To find the optimal translation u to account for normal
offset
hi
at each sampling point whose image normal direction is
ni,
we solve the following equation:
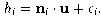 (7)
(7)
minimizing ei.
Once the translation has been calculated, the other
components are estimated. It is assumed that the
distortion is centred about the tracker's local origin (normally its
centroid, to optimally decouple it from translation).
The effects of
translation
ni . u
are subtracted from each normal
offset, leaving a residual offset. We can then find the matrix A
that
maps image coordinates to displacement:
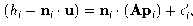 (8)
(8)
where pi
is the sampling point's position relative to the local
origin and ei
is again the error term to be minimised.
In practice this formulation can lead to
problems when the tracked
surface moves whilst partially obscured (often, a tracker will catch
on an occluding edge and become `squashed' as it passes in front of
the surface). It can also be unstable and sensitive to noise
when the tracker is long and thin.
We therefore use a simplified approximation to
this equation that ignores the aperture problem (equating the
normal component with the whole displacement):
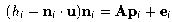 (9)
(9)
ei
is an error vector, and our implementation solves the equations to
minimise its square magnitude.
This produces a more stable tracker that, although sluggish to deform,
is well suited to those practical tracking tasks where motion
is dominated by the translation component.
The tracker positions are updated from u and A
using a real time first-order predictive
filter. This enhances performance when tracking fast-moving objects.
Next
Contents


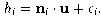 (7)
(7)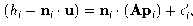 (8)
(8)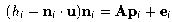 (9)
(9)