Appendix: Comparison of full-perspective and affine stereo

A.1 Correspondence and the epipolar constraint

In the affine stereo formulation it was assumed that two sets of image coordinates were available for each world point. The task of identifying pairs of image features which correspond to the same point in space is known as the correspondence problem.

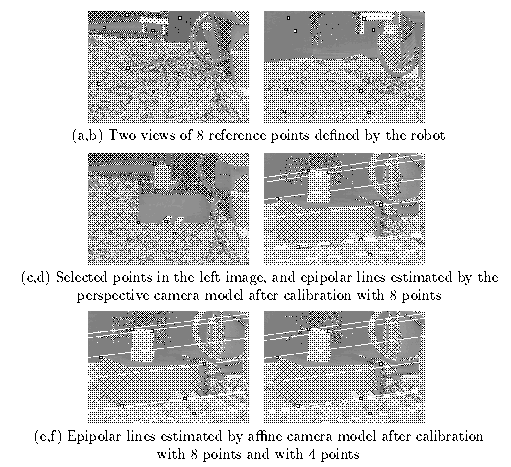
The image coordinates of a world feature in two images are not independent, but related by an epipolar constraint. Consider the family of planes passing through the optical centre of each camera. These project to a family of epipolar lines in each image. If a feature lies upon a particular line in the left image, the corresponding feature must lie upon the line in the right image, which is the projection of the same plane. The constraint reflects the redundancy inherent in deriving four image coordinates from points in a three-dimensional world. Most correspondence algorithms exploit this constraint, which reduces the search for matching features to a single dimension, and identifying it is an important aspect of any calibration scheme.

In affine stereo, the epipolar planes are considered to be parallel, and the constraint takes the form of a single linear relation among the four image coordinates. With the full perspective model, the lines need not be parallel, and converge to a point called the epipole (the projection of one camera centre on the other camera's image plane). The constraint may be obtained from calibration data, for instance by rearranging the model to predict one image coordinate as a function of the other three.

Figure 7 compares the epipolar line structure predicted by both affine and full perspective stereo models (after calibration using linear least squares). In this setup, in which the camera distance is about 2 metres, both models give similar epipolar accuracy. Furthermore, the affine model can predict epipolar lines using just 4 reference points; perspective stereo requires a minimum of 6.


Figure 7: Estimation of epipolar lines. Although it considers the epipolar lines to be parallel, the affine camera model (e) is almost as accurate as perspective in this experiment (RMS perpendicular error 4.1 pixels). Even with only 4 reference points, it produces a reasonable solution (f) from which stereo correspondence could be performed (RMS error 6.2 pixels).

A.2 Accuracy of reconstruction

To compare affine and full perspective stereo, we performed a series of numerical simulations, measuring their ability to estimate the relative positions of points within a workspace, viewed by a pair of pinhole cameras.

[Reference and test points are confined to a unit cube centred about the origin. There are 6 reference points within the unit cube. Test points are distributed uniformly within the cube. The cameras face the origin from a distance of 3-24 units, angled 20 degrees apart (their focal length is proportional to distance, to normalize image size)].

  • Under ideal conditions:

    Without noise or other disturbances, perspective stereo estimates absolute and relative positions with complete accuracy. At close range affine stereo performs poorly, but the error decreases in inverse proportion to camera distance (figure 8).

    Accuracy is also somewhat dependent on the number and configuration of the reference points used in calibration, and there is a limited improvement as the unit cube is sampled more regularly.

  • With noisy calibration data:

    Adding 1% Gaussian noise to the image coordinates of the reference points causes both systems to lose accuracy. Perspective stereo is more sensitive to noise because of its nonlinearlity and greater degrees of freedom, and is less accurate than the affine stereo approximation at large viewing distances (figure 9). (viewing a larger number of reference points reduces the effects of noise and restores the accuracy of perspective stereo).

  • Camera movements after calibration:

    In a laboratory or industrial environment it is possible for cameras to be disturbed from time to time and subject to small rotations and translations. If this happens after calibration, it will give rise to a corresponding error in stereo reconstruction.

    Table 1 shows the average change in perceived relative position when one camera is rotated or translated a small distance around/along each principle axis. The two systems degrade comparably with small movements, the worst of which is rotation about the optical axis. Perspective stereo is more sensitive to larger movements, and to rotations and translations in the epipolar plane (in which a small error can induce large changes of perceived depth), because it distorts nonlinearly.

  • With noisy image coordinates:

    When gaussian noise is added to the image coordinates of the points whose relative position is to be estimated (after accurate calibration), the effect is comparable on both systems, and their performance converges at large camera distance (figure 10).


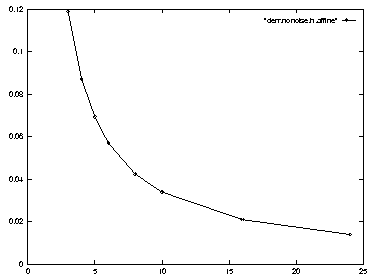
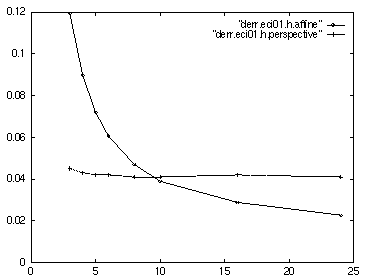
    Figure 8: RMS relative positioning error (for random point pairs in the unit cube) as a function of camera distance. The error is due to the approximate nature of the affine stereo model and drops as camera distance increases.


    Figure 9: RMS positioning error as a function of camera distance, after calibration with noisy reference point images (standard deviation 1% of image size). The error suffered by the perspective model (dotted) is comparable in magnitude to the affine stereo systematic error.


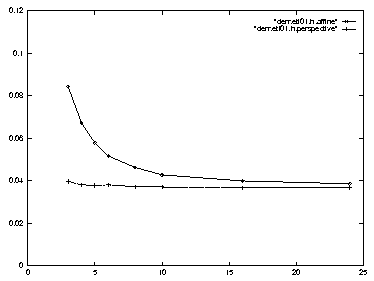
    Figure 10: RMS relative positioning error from noisy images (standard deviation 1% image size) of world points after accurate calibration with 27 reference points. The two models converge for camera distances above about 10 units.


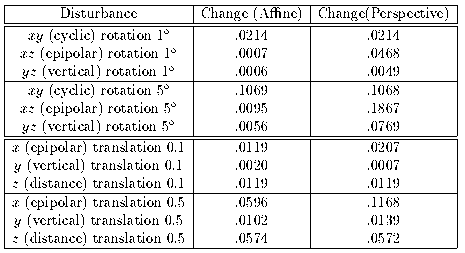
    Table 1: RMS change to relative position estimates of world points, caused by disturbing one of the cameras after calibration.
  • Contents