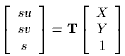 (1)
(1)
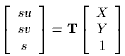 (1)
(1)
Now, given the image coordinates of a point anywhere on the plane, along with the image coordinates of the four reference points, it is possible to invert the relation and recover the point's working plane coordinates, which are invariant to the choice of camera location [7]. We use the same set of reference points for a stereo pair of views, and compute two transformations T and T', one for each camera.

Figure 1: Relation between lines in the world, image and ground planes. Projection of the finger's image line li onto the ground plane yields a constraint line lgp on which the indicated point must lie.
Repeating the above procedure with the second camera C' gives us another view li' of the finger, and another line of constraint lgp'. The two constraint lines will intersect at a point on the target plane, which is the indicated point. Its position can now be found relative to the four reference points. Figure 2 shows the lines of pointing in a pair of images, and the intersecting constraint lines in a `canonical' view of the working plane (in which the reference point quadrilateral is transformed to a square). This is a variation of a method employed by Quan and Mohr [8], who present an analysis based on cross-ratios.
By transforming this point with projections T and T', the indicated point can be projected back into image coordinates. Although the working plane coordinates of the indicated point depend on the configuration of the reference points, its back-projections into the images do not. Because all calculations are restricted to the image and ground planes, explicit 3-D reconstruction is avoided and no camera calibration is necessary. By tracking at least four points on the target plane, the system can be made insensitive to camera motions.
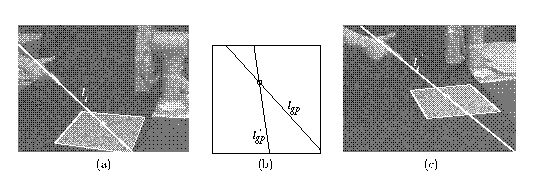
Figure 2: Pointing at the plane. By taking the lines of pointing in left and right views (a, c), transforming them into the canonical frame defined by the four corners of the grey rectangle (b), and finding the intersection of the lines, the indicated point can be determined; this is then projected back into the images.